Jonathan Hermon: The exclusion process mixes (almost) faster than independent particles

2019. 10. 21. 16:15 - 2019. 10. 21. 17:45

Esemény típusa: szeminárium

Szervezés: Intézeti

Kutszem

Leírás

Előadó: Jonathan Hermon

Cím: The exclusion process mixes (almost) faster than independent particles

Absztrakt:

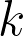The exclusion process is one of the most basic and best studied processes in the literature on interacting particle systems, with connections to card shuffling and statistical mechanics. It has been one of the major examples driving the study of mixing-times. In the exclusion process on an $n$ -vertex graph we have $k$ black particles and $n-k$ white particles, one per site. Each edge rings at rate 1. When an edge rings, the particles occupying its end-points switch positions. 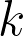Oliveira conjectured that the order of the mixing time of the process is at most that of the mixing-time of $k$ independent particles. Together with Richard Pymar we verify this up to a constant factor for $d$ -regular (or bounded degree) graphs 1 in various cases:

(1) the degree $d$ is at least $\Omega (\log_{n/k} n)$ , or

(2) the spectral-gap of a single walk is small (at most log number of vertices to the power 4), or

(3) when the number of particles 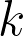$k$ is roughly $n^a$ for some constant $0<a<1$ .

In these cases our analysis yields a probabilistic proof of Aldous' famous spectral-gap conjecture (resolved by Caputo et al.).

We also prove a general bound which (when $k > n^c$ ) is within a $\log \log n$ factor from Oliveira's conjecture. As applications we get new mixing bounds:

(a) $O(\log n \log \log n)$ for expanders,

(b) order $\log (dk)$ for the hypercube $\{0,1\}^d$ and

(c) order $(\text{diameter})^2 \log k$ for vertex-transitive graphs of moderate growth and for the giant component of supercritical percolation on a torus.